だれでも試せる因子分析(まずはR編)

※注意)弊社代表の独断と偏見です。
だれでも試せる因子分析(まずはR編
今回のテーマ
だれよりも最速に、そして最短で因子分析を試してみたいと思います。
今回は、「R」の開発実行環境を利用させていただきます。
細かい解説は必要最小限度にします。
Rとは
オープンソース・フリーソフトウェアの統計解析向けのプログラミング言語及びその開発実行環境
因子分析とは
多変量データに潜む共通因子を探り出すための手法
『https://www.macromill.com/service/data_analysis/d008.html』
今回は、集計したアンケート結果から、その背後に隠れている回答者たちの「想い」を可視化します。
|手順
- アンケート結果CSVファイルを用意
- Rへの接続
- R: CSVの読み込み
- R:データの相関行列を算出する
- R:行列の固有値および固有ベクトルを算出する
- R:共通因子数のあたりをつける(スクリープロット)
- R:因子分析を実施する
- 描画
|アンケート結果CSVファイルを用意
・アンケート結果の参考書籍『マンガでわかる統計学 因子分析編』
・アンケートファイルダウンロード 因子分析 名前「因子分析.csv」
アンケート内容は、喫茶店へ来店されたお客様へ、6つの質問を5段階で回答させたものです。因子分析を前提に考える場合、後処理を考えて、アンケート設計がとても重要です。そう考えると、世の中のアンケートのほとんどは、思いつきで作ったアンケートが多いのではないでしょうか?今後、ぜひ、因子分析を前提に考えてみましょう!
|Rへの接続
あらためて解説するまでもなく、たくさん、参考文献があります。
ぜひ、そちらを活用ください。
|R: CSVの読み込み
対象アンケートCSVファイル位置は下記の通りです。
要は、デスクトップに配置した状態です。
web-kaizen$ pwd
/Users/toshiya.murayama.web-kaizen/Desktop
murayamatoshiya-no-MacBook-Pro:Desktop toshiya.murayama.web-kaizen$ ls
因子分析.csv
csv<-read.csv(file=”/Users/toshiya.murayama.web-kaizen/Desktop/因子分析.csv”,header=T, fileEncoding=”utf8″,row.names=1)
|R:データの相関行列を算出する
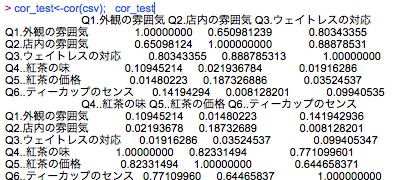
cor_test<-cor(csv); cor_test
|R:行列の固有値および固有ベクトルを算出する

eigen_test<-eigen(cor_test)$values; eigen_test;
|R:共通因子数のあたりをつける(スクリープロット)
![]()
plot(eigen_test,type=”b”,main=”Scree Plot”, xlab=”NUM”, ylab=”VALUE”)
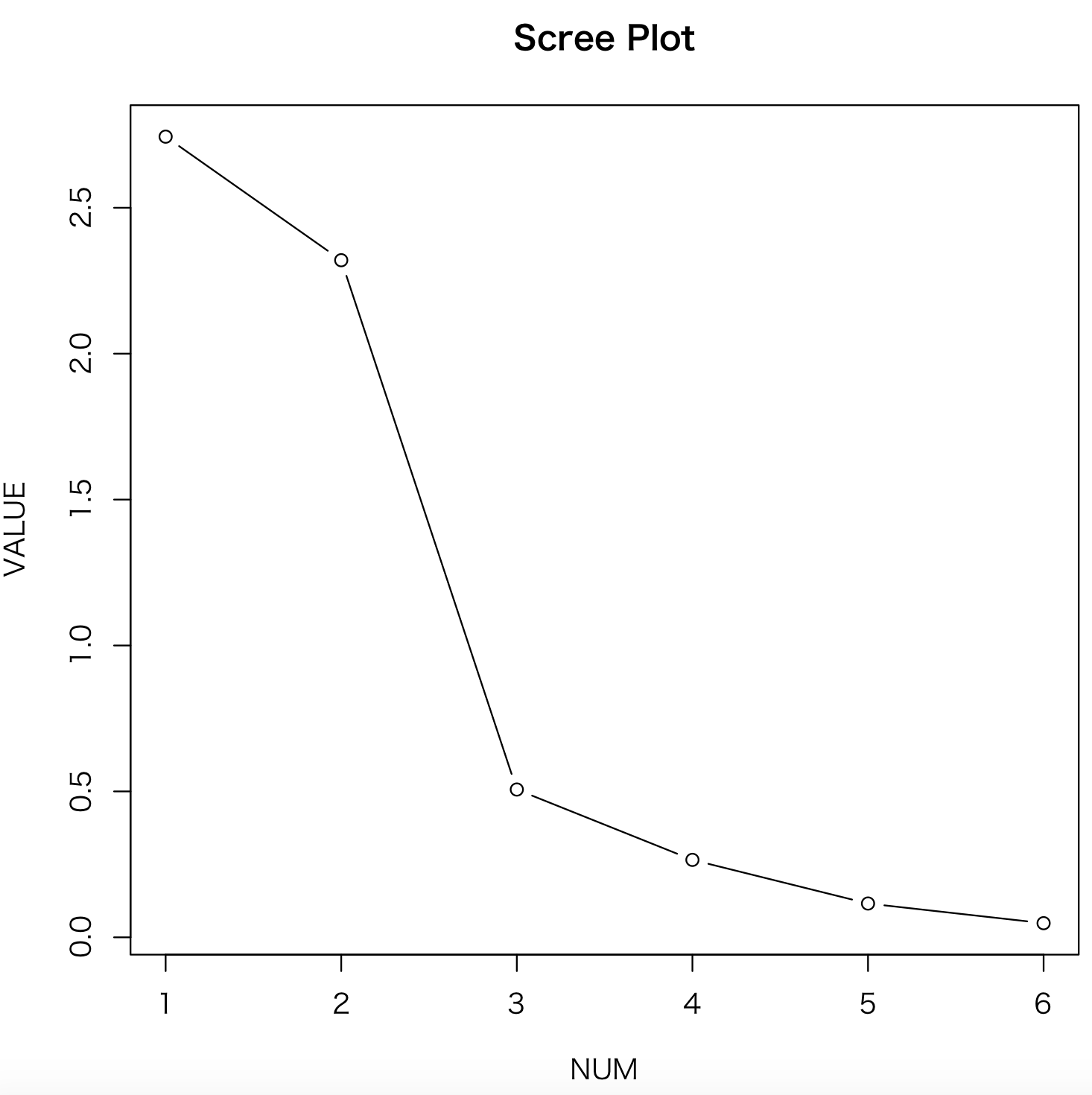
1より大きい固有値の数とスクリープ ロットにおける固有値の減衰をみて
共通因子 の数を2が良さそうと判断する
|R:因子分析を実施する
・factanal()を使う
・回転はvarimaxを選択する
・因子負荷量は最尤法を使う
・回帰方法はBartlettを使う

result<-factanal(x=csv,factors=2,rotation=”varimax”,scores=”Bartlett”);
独立因子 Uniquenesses:
因子負荷量 Loadings:
寄与度 SS loadings
寄与率 Proportion Var
累積寄与率 Cumulative Var
因子得点 scores
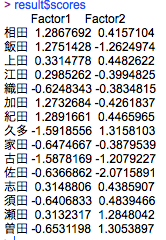
> result$scores
因子負荷量
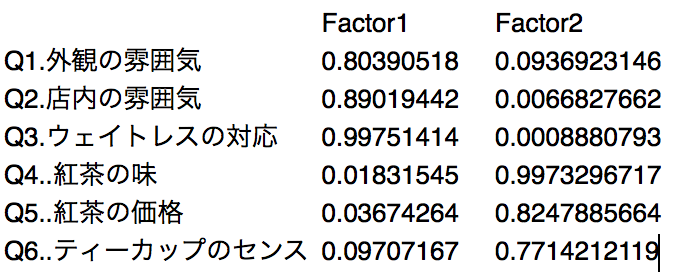
unclass(result$loadings)
|描画
biplot(result$scores,result$loading,cex=2)
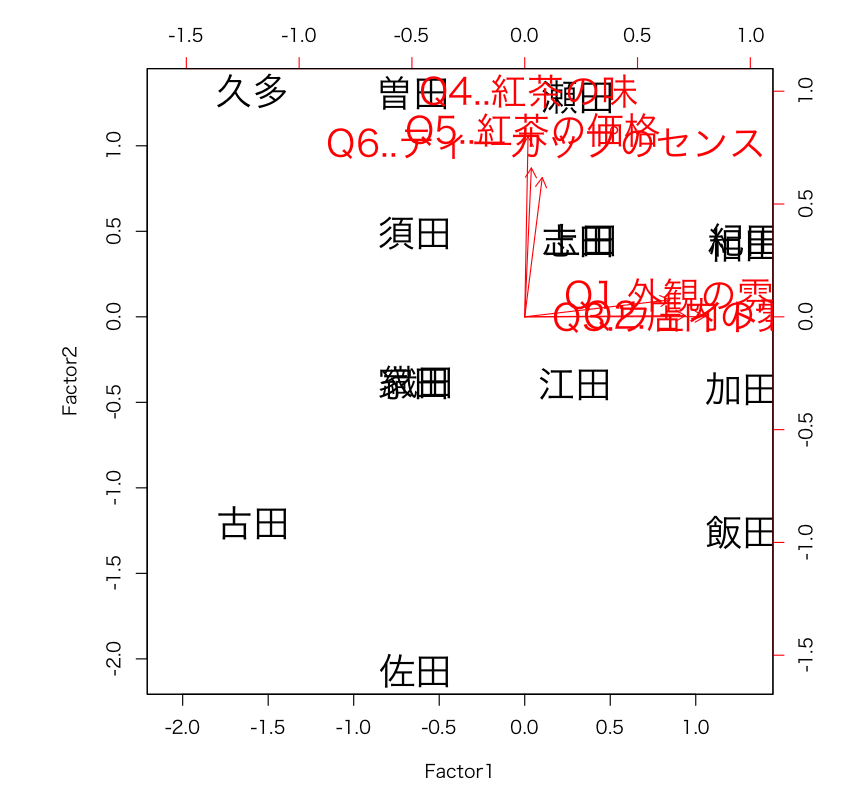
解釈)
まず、factor1の因子負荷量を確認します。おおよそ、0.5以上を目安にします。
因子負荷量の絶対値が大きいほど、影響を及ぼしているといえます。
factor1では、Q1,Q2,Q3が影響を及ぼしていると言えそうです。
次に、factor2をの因子負荷量を確認します。同じように、0.5以上を目安にします。
そうすると、Q4,Q5,Q6が影響を及ぼしていると言えそうです。
Q1,Q2,Q3のfactor1はひとことで言うと・・・ → 雰囲気
Q4,Q5,Q6のfactor2はひとことで言うと・・・ → 紅茶
と言えそうです。
つまり、この喫茶店では、「雰囲気」と「紅茶」が大事では?と言えそうです。
この時の分析精度を確認するには、累積寄与率を確認します。
factor2(第二共通因子)までの累積寄与率は、0.787です。
0.5は欲しいところですので、分析はうまくいっていると言えそうです。
そして、各factorの因子得点をみると・・・
factor1のもっとも得点が高い人 → 紀田さん
factor2のもっとも得点が高い人 → 久多さん
この2名はそれぞれの共通因子に対する満足度は高そうですね。
いずれにせよ、このアンケート結果から見えてきたのは、”雰囲気”と”紅茶”の2つはこの店にとって大事な要素といえるでしょう。
|まとめ
本日は、Rの因子分析を試してみました。
この解説を理解すれば、明日からのアンケート業務もかなり意味のある、楽しい作業になるのではないでしょうか?
また、単純にアンケートを作ってはいけないこともこれでよくわかると思います。
ぜひ、明日のセミナーアンケートから、アンケート設計と分析を楽しんでください!
当然、次は、Tableau x R連携ですね!
(ここへのつなぎのための記事でした)
文責:村山 敏也 監修:なし