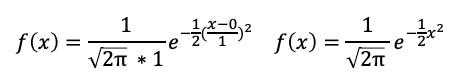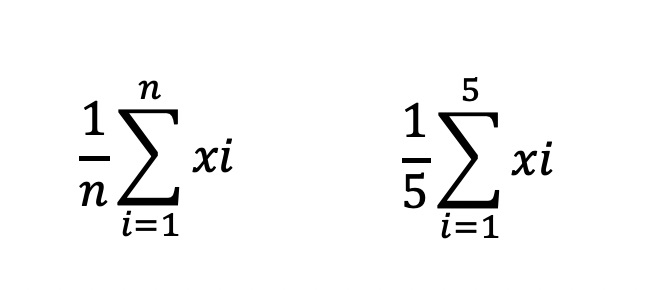統計をはじめるにあたって(全体アウトライン)

統計をはじめるにあたり(全体アウトライン)
統計学の基礎知識を身につけるためのアウトラインは…
まずは、下記のアウトラインを使って情報収集し、知識を整理しながら肉付けしていく流れになるかと思います。統計学は正確性を重視するあまり、かえって説明がややこしくなる傾向があります。多少の誤解を恐れず、大胆におおざっぱに説明してくれる方を最初にメンターにすると良いと思います。YouTube動画などの解説動画を利用するのも一つの選択肢だと考えます。
(1)統計学の分類
(2)統計で扱うデータの分類と定義
(3)グラフ(割合・相関・箱ひげ図・度数分布・ヒストグラム・クロス集計)
(4)代表値(平均値・中央値・最頻値)
(5)偏差・分散・標準偏差・データ正規化・変動係数と偏差値
(6)相関・外れ値
(7)サンプル・母集団・標本誤差・確率・正規分布・確率密度関数
(8)中心極限定理
(9)標準誤差と95%信頼区間
(10)仮説検定・P値・過誤 etc
(11)統計でよく出てくる計算
(12)統計でよく出てくる記号
下記各項目に対する詳細事項は後日、別のページで後述しますが、取り急ぎ、統計に関する知識を整理・肉付けするために必要なトピックだけを先に提示しておきます。※ところどころ、誤解を恐れず端折っております。
(1)統計学の分類
統計学の分類
おおまかに下記のように捉えられると良いでしょう。アカデミックな領域ですので位置付けだけおおまかに掴んでおくだけで良いと思います。
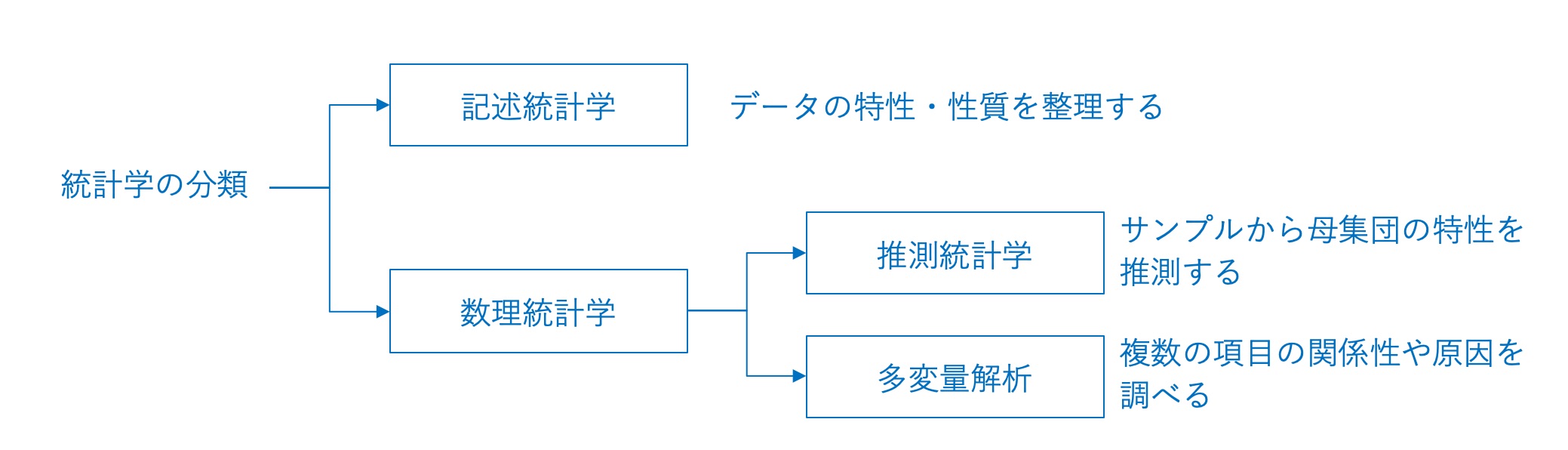
a) 記述統計学と数理統計学(推測統計学・多変量解析)
記述統計学は、観測対象となった手元のデータをグラフ化(データビジュアライゼーション)し、あるいは、平均、中央値または最頻値などの「代表値」や標準偏差などを使い、データを整理したり分布状況を把握します。そこからデータの特徴・性質を見つけることを目的としております(整理と要約)。ポイントは、Rawデータ(生データ)から情報を削ぎ落としながらも特徴・性質を浮き上がらせる引き算の作業をしている点にあります。これに対して、推測統計学は、サンプルから母集団の特性を推測することを目的としております。なお、多変量解析とは、複数の変数を同時に扱って因果関係の解明、予測、分類などを目的としております。ただし、因果関係自体を解明できない場合も多いです。
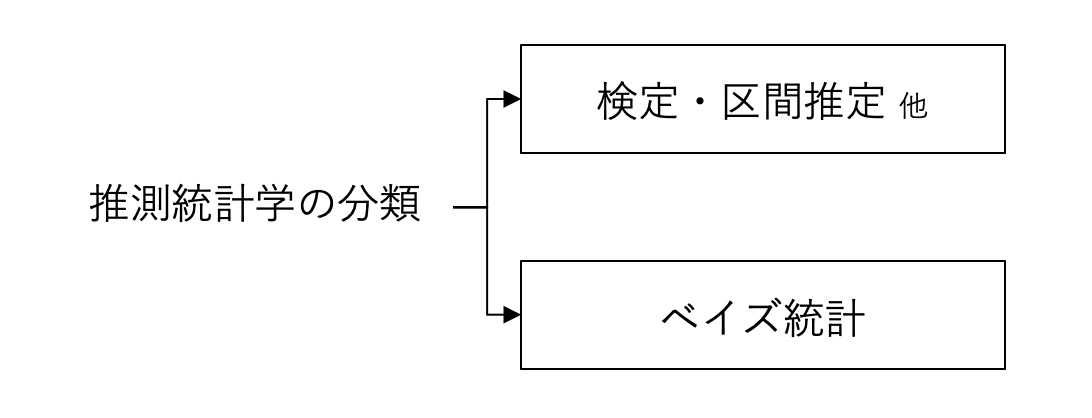
b) 推測統計学の分類
ベイズ統計を推測統計学に含めない考え方もあるようです。なぜならば、ベイズ統計は、標本を必ずしも必要としないという向きもあるから、とのことです。こちらの分類方法は参考までにとどめておけば良いでしょう。
(2)統計で扱うデータの分類と定義
データの分類
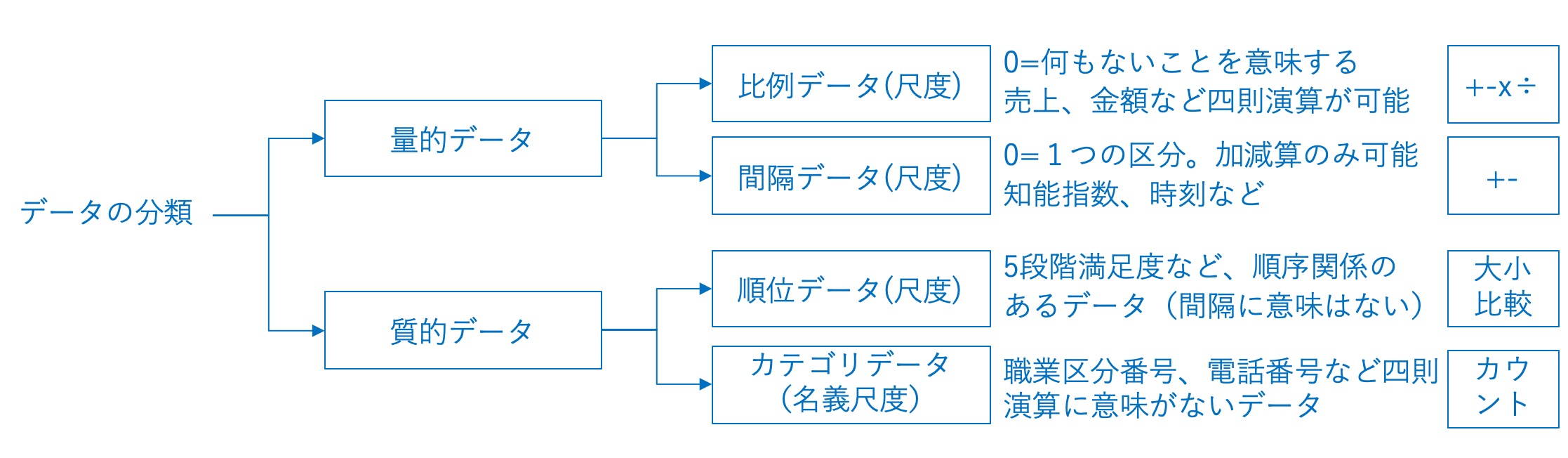
大きく、量的データと質的データで分類されます。この分類によって、そのあとの統計手法が異なります。
a) 量的データの分類
量的データは、一般的には測れるデータ(数量データ)などと呼ばれ、比例データ(比例尺度)と間隔データ(間隔尺度)に分類されます。
・比例データ(比例尺度):売上(金額)など、0=何もない事を意味し、かつ、四則演算に意味をなすようなデータ。等間隔であり、倍数関係がある。比例データで取り扱う代表値は、各種平均値。
・間隔データ(間隔尺度):0はあくまで区分の一つとして捉えられ、加減算のみ意味をなすようなデータ。等間隔ではあるが、倍数関係がない。例としては、時間などがわかりやすい。時間の0は、何もない事を意味しているわけではない。一つの状態を指している。このようなデータは加減算は有効だが「乗除」はまったく意味をなさない。間隔データで取り扱う代表値は、算術平均。
b) 質的データの分類
質的データは、一般的には測れないデータ(カテゴリカルデータ)などと呼ばれ、順位データとカテゴリデータに分類されます。
・順位データ(順位尺度):5段階満足度アンケートなど、1,2,3,4,5など順位付け自体には意味をなすが間隔自体は意味をなさない。例えば、2は4の半分の満足感しかない、といわれると程度(間隔)が半分かどうかは人により定かではない。そのため、大小の比較はできても四則演算は意味をなさないデータ。順位データで取り扱う代表値は、中央値・最頻値。
・カテゴリデータ(名義尺度):職業区分コード(001:農業…)など、大小関係もなく、内容を区別するだけに用いられるデータ。四則演算しても意味をなさない。カテゴリデータで取り扱う代表値は、最頻値。
c)離散データと連続データ
特に、連続データでは、確率で重要になります。なお、一般的には、データを「変数」と呼びます。
離散データ:とびとびの数値で表されるデータをいう
例)サイコロの目、人数、年齢、テストの点数
連続データ:連続的数値で表されるデータをいう
例)身長、体重、時間
d)データの次元について
データの次元は、変数の個数で決まります。変数が1つの場合、1次元データ、2つの場合、2次元データあるいは3つの場合は3次元データ(多次元データ)となります。
(3)グラフ(割合・相関・箱ひげ図・度数分布・ヒストグラム・クロス集計)
通常、データを収集した場合に行う第一歩としては、分布やばらつきをざっと見ることが多いかと思います。※ データ分析する前の習慣 をご一読ください。記述統計学の最初の一歩は、収集したデータを整理して、さまざまなグラフで作図してみることです。その結果、その特性・性質を炙り出すことに繋がります。
グラフの主な種類
a) 量的差異を表現する棒グラフ
b) 時間的経過(トレンド・推移)や変化などを表現する折れ線グラフ
c) a)やb)を同時に表現する複合グラフ(共有軸、二重軸)
d) 全体に対する比率や割合を長方形で表現する100%積上棒グラフ
e) 割合を円で表現する円グラフ
f) すべての要素に対して全体の割合を矩形で表現するツリーマップ
g) 2つの値の関係性を表す散布図・バブルチャート
散布図は外れ値も同時に確認可能。量的データ * 量的データはまずは散布図で確認する。
h) 複数の項目の状態を俯瞰できるレーダーチャート・ハイライト表
i) 適当な間隔で頻度(度数)を表す度数分布・相対度数分布・累積度数分布
階級:特定の範囲(値段100円-200円など)で区切られたもの。ビンとも呼ぶ。階級の個数はスタージェスの公式を使って求める(とされている)。
階級幅:階級の幅のこと。上の値段の例では「100」が階級幅。ビンのサイズとも呼ぶ。
階級値:階級のちょうど真ん中の値
度数:各階級に属する「データ個数」のこと
相対度数:各階級に属する「データ個数」/ 全体のデータ個数 cf 確率と同一視できる
累積度数:度数の累計
累積相対度数:累積度数 / 全体のデータ個数
j) 度数分布表をグラフ化したヒストグラム・度数折れ線
ヒストグラムの条件:縦軸に度数または相対度数 横軸に変数
ヒストグラムの役割:分布を把握する目的で使う
ヒストグラムの見方:分布を解釈するためには下記3つを評価すると良い
①山の数 :単峰性(1つ山)、二峰性(2つ山)、多峰性(複数山)
二峰性あるいは多峰性の場合、性質の違う集団が混在している可能性がある。
統計は単峰性を前提としているため、混在している性質の違う集団(男性・女性など)を分けていく必要がある。
②分布形状 ベル型分布、左右に裾が長い分布、べき分布・パレート分布
③広がりの範囲
k) 散らばりと外れ値を表現する箱ひげ図・バイオリン図
箱ひげ図は複数対象の分布の比較に向いている。量的データ*質的データの場合は箱ひげ図で可視化するとより理解が深まる。
l) 2つの変量の正確な数値を可視化するクロス集計・テーブル表
質的データと質的データを可視化する場合は、クロス集計を検討すると良い。
(4)代表値(平均値・中央値・最頻値)
統計学では、まずは下記3つがもっとも重要な値となります。この3つの値を「代表値」と呼びます。ここでは、代表値としてふさわしい値が必ずしも平均値とは限らない点を理解しておくと良いでしょう。
a) 平均値(mean) データの合計をデータ個数で割った値(データ個数1単位あたりの数値)。
b) 中央値(median) データを大きさの順に並べた後、ちょうど真ん中にあたる値。※ データの個数が偶数の場合は、さらに真ん中2つの値を平均した値が中央値となる
c) 最頻値(mode) もっとも頻度(度数)の多いデータの値。質的データの代表値。
※ なお、a)の平均の種類は複数ありますのでこちらでご確認ください。
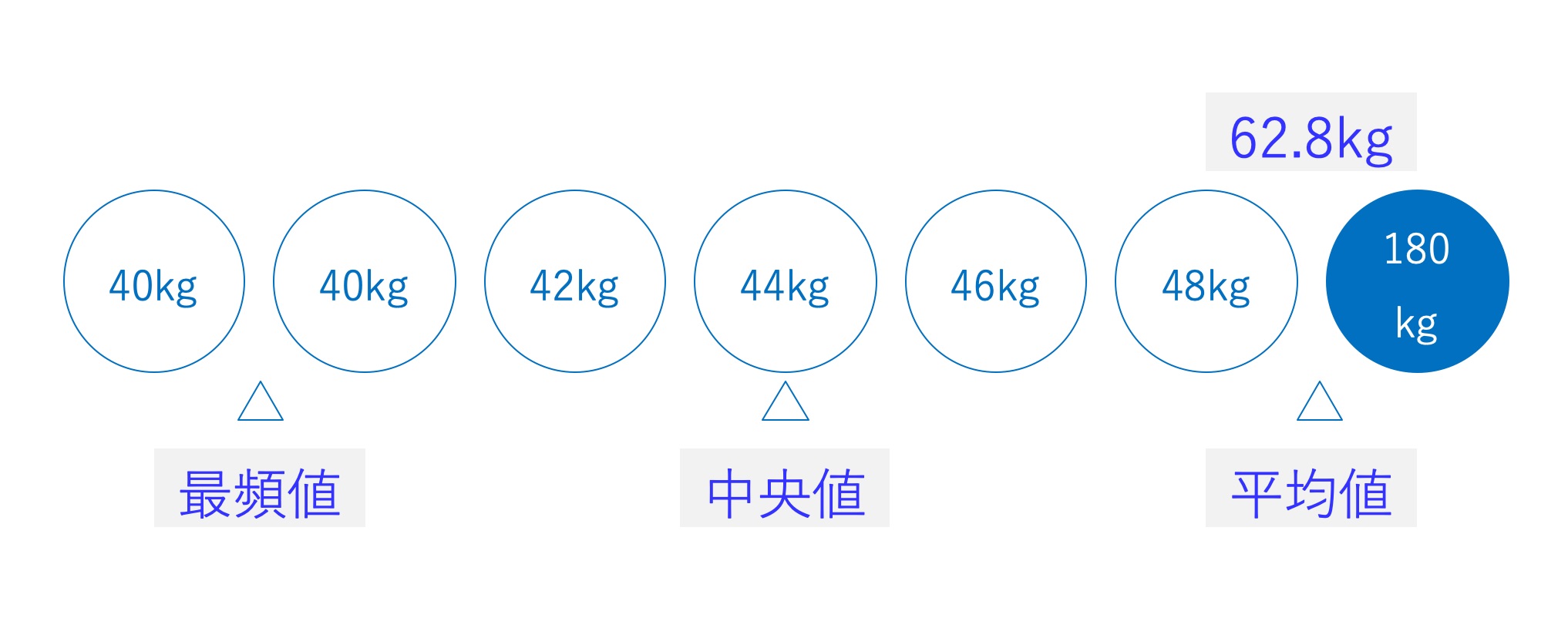
それぞれの値のデメリット)
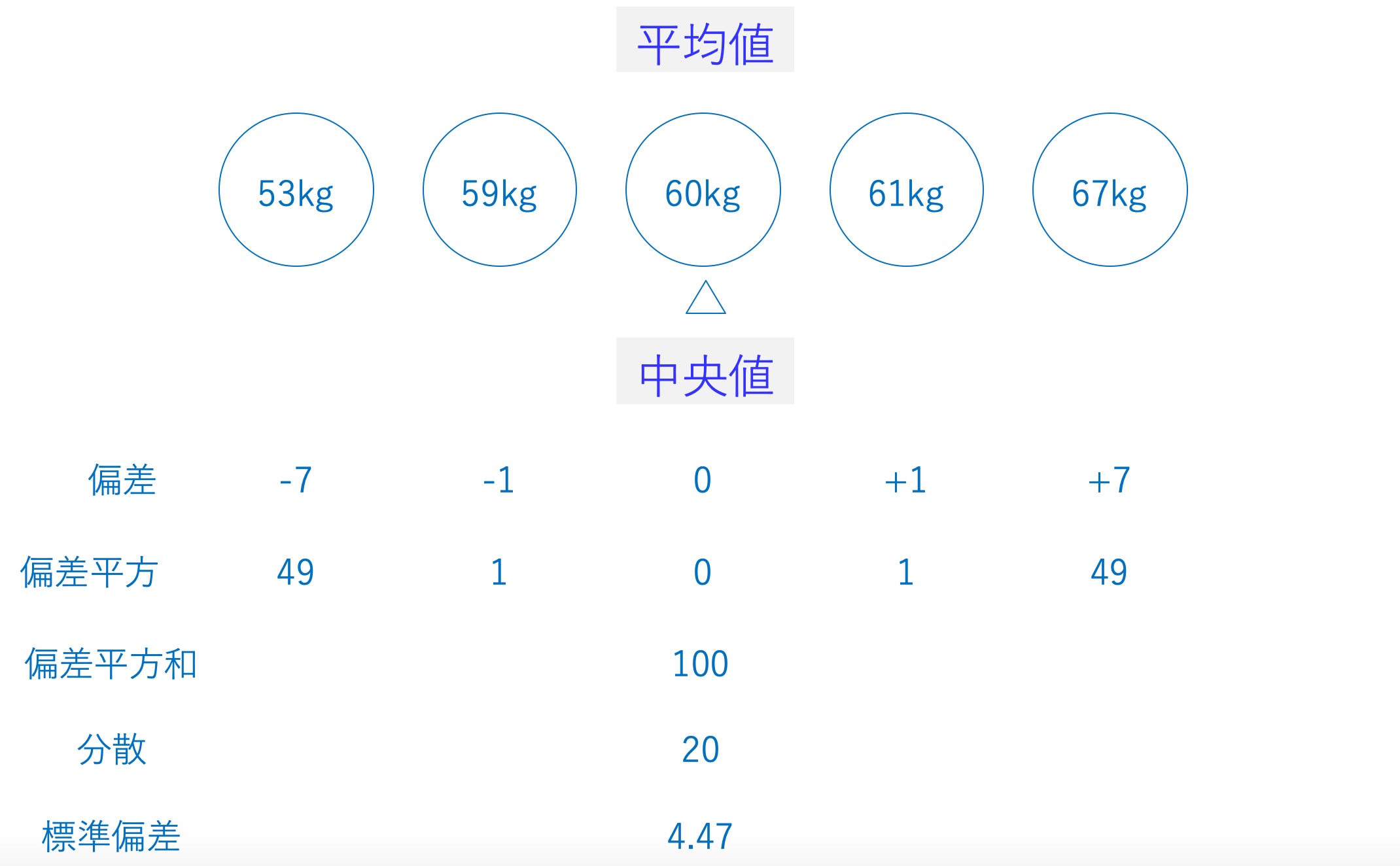
例えば、以下の体重データ(女性)をもとにパーティーのメニューを準備しようとします。a)平均値だけで見た場合、少しボリューミなーメニューを用意しないと不満が出そうだなと予測しそうですが果たしてそれは正しい予測でしょうか?。逆に、b)中央値だけで見た場合、1人だけおやつ分にも満たないくらいのボリュームとなってしまいそうです…。これも少々バランスを欠いた予測といえるでしょう。
a) 平均値 極端な数値に引きずられてしまう特性がある ※ 平均は悪か?
b) 中央値 極端な数値にほとんど影響を受けない反面、データ全体傾向が推測しづらい面もある
c) 最頻値 そもそもすべて頻度が1であれば意味をなさない
(5)偏差・分散・標準偏差・データ正規化・変動係数と偏差値
基本的にデータはばらつくものと考えてください。実際、どれくらいばらついているかを調べることが大切です。実際、統計の世界では、平均そのものよりも、平均からの差(偏差)に着目します。そこで、このばらつきを数値化する場合、一般的に以下のプロセスを踏みます。ここで基準となるのが算術平均です。この算術平均をもとに、偏差、分散、標準偏差や偏差値を導いていくようにします。
<偏差から標準偏差までの流れ>
a) 偏差(=平均からの差)を可視化する
偏差 = データ値 – 平均値
※ + や – が出てくるのが特徴。全部足したり(=偏差の総和)平均すると結局0になる。
b) 偏差平方和(=それぞれの偏差を2乗して合計する)を可視化する
偏差平方和 = 「それぞれの偏差(=平均からの差)2」 を出して合計する
※ 偏差は + や – があるため、一旦、2乗します。これらをすべて合計したものを偏差平方和と呼びます。
c) 分散(=偏差平方和をデータ個数で割る)を可視化する
分散 = 偏差平方和 / データ個数
※ データ個数で割る意味は、データ個数1単位あたりの数に引き直すため。これにより、複数のグループのデータ個数が異なっても問題なくなる。
※ データの個数(N)で割る場合と、データの個数(n-1)で割る場合があるが前者は母集団を、後者は標本調査(この場合は不偏分散と呼ぶ)で使い分けする。
※ 偏差の平方の平均。この平均は注意が必要。偏差が大きければ当然分散の値は大きくなるものの、そもそも単位(cmとmなど)が異なる場合、これだけではばらつきの大小は判断できないため、次の「標準偏差」を使って元の単位に引き戻します(cm2→cmなど)。
※ 標準偏差の2乗でもある。
d) 標準偏差(=分散の√ )を可視化する
標準偏差 = √ 分散 (平方根)
標準偏差 = √ ((個々のデータ – 平均)2 を足したもの / データの個数)
※ 平方根(ルート)を採るのは、偏差のもともとのスケールに引き直すため。
※ 元のデータと同一の単位でばらつきの平均を表す指標。
※ 最小値が0であり、散らばりの程度が大きいほど、標準偏差も大きな値となる。
※ 1データあたりの平均からのズレを表す指標ともいえる。
<データ正規化(標準化)・変動係数>
データの標準化は、端的に述べると、どのようなデータでも同じ横軸・縦軸を使って比較できるようにすることです。
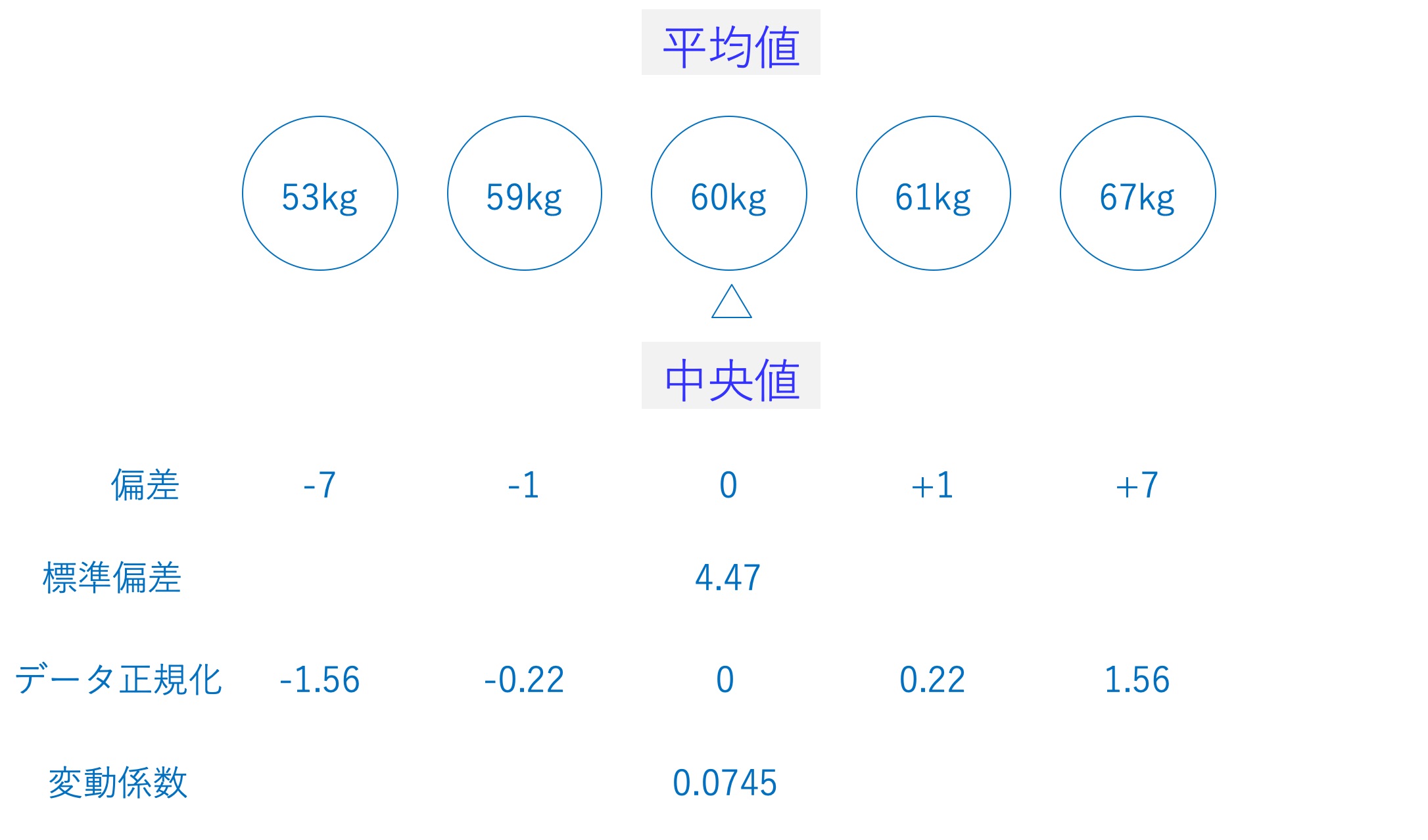
e) データ正規化(標準化)を可視化する(基準化ともいい、基準化されたデータを基準値という)
データ正規化を実施することで、満点が異なるまたは、単位が異なる変数の比較が可能。偏差は標準偏差の何倍かを求めている。
データ正規化 = (個々のデータと平均からの差:偏差) / 標準偏差
※標準化後は、平均が0、標準偏差は1になる
※ 平均を0、標準偏差を1に変換することであらゆるデータを同じ基準にすることが可能
※ A教科の平均40点(標準偏差20)で60点を取った場合とB教科の平均80点(標準偏差10)で90点取った場合とでは価値は同じ(データ標準化の値はそれぞれ1である)。
※ 例えば、A教科とB教科の平均点数が同じでかつ、それぞれテスト得点が同じだった場合でも、データの散らばり程度が小さい方が価値は高くなる(=偏差は標準偏差の何倍か?)
f) 変動係数 を可視化する
変動係数 = 標準偏差 / 平均
※ 異なる単位をもつグループ同士を比較するために使用する
g) 偏差値 を可視化する
偏差値 = データ正規化 * 10 + 50
※ 平均点をとった人の偏差値をちょうど50にして、グループの中での位置付けを表す。いいかえると、満点が何点でも、あるいはどのような単位の変数でも、その偏差値の平均は必ず50となり、標準偏差は必ず10となる。
(6)相関・外れ値
(5)のセクションは1つの変数について求める1変量統計となります。(6)のセクションは、2つの変数について求める2変量統計です。
a) 相関について
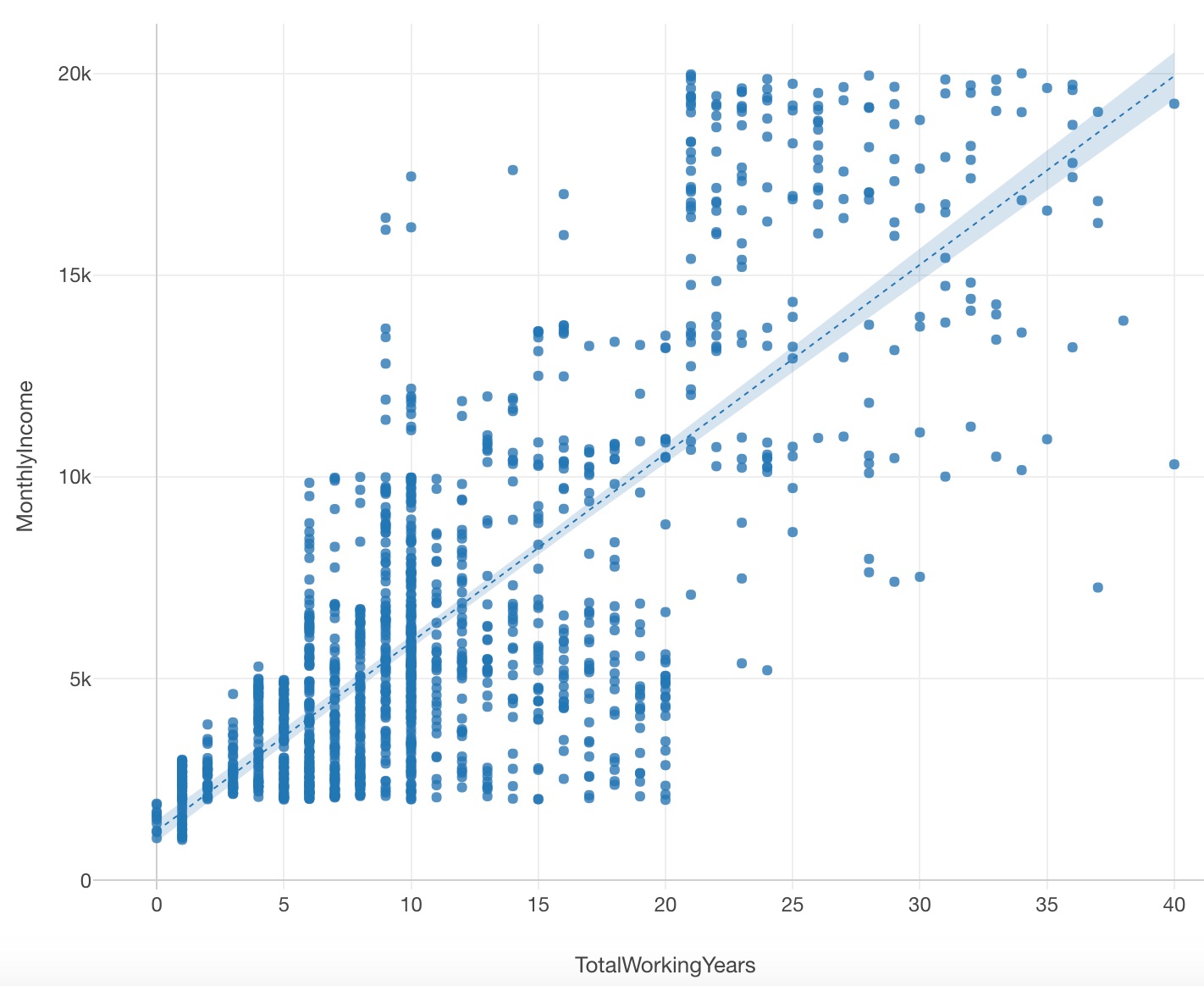
2つの変数のうち、一方が増えると他方も増えるという関係がある場合、それを正の相関と呼びます。逆に、一方が増えると他方が減るという関係を負の相関と呼びます。なお、原因となる変数を説明変数と呼びX軸側に配置します。他方、影響を受ける側を目的変数としてY軸側に配置します。もし、強い相関関係を見つけることができれば、この目的変数を予測することが可能となります。なお、2変数の組み合わせとしては、数量と数量(散布図&単相関係数を使う)、数量とカテゴリデータ(箱ひげ図&相関比を使う)、カテゴリデータとカテゴリデータ(クロス集計&クラメールの連関係数を使う)の3パターンが考えられます。
相関係数)
相関の強さをを表す統計量。r で表記する。通常、取り得る範囲は-1から1の範囲。0に近ければ近いほど、おおむね、相関は弱い(もしくは無い)と判断できる。正の相関の場合、+1に近づき、負の相関の場合、-1に近づく。一般的には、ピアソンの積率相関係数をさす。厳密にいうと、数量と数量の場合、ピアソンの積率相関係数(単相関係数)(-1から+1)、数量とカテゴリデータの場合、相関比(0から+1)、カテゴリデータとカテゴリデータの場合、クラメールの連関係数(0から+1)を求めます。
ピアソンの積率相関係数 = 共分散 / (xの標準偏差 * yの標準偏差)
共分散 = ((x1の偏差)(y1の偏差)+(x2の偏差)(y2の偏差)+…(xnの偏差)(ynの偏差))/データ個数
→ ざっくりいうと、共分散は、(Xの偏差)(Yの偏差)の平均といえる
→ (xnの偏差)(ynの偏差) は偏差同士の積
R2乗値)
決定係数と呼ぶ。回帰式(予測式)の精度を表す指標。おおむね、相関係数の二乗したものと一致する。取り得る範囲は、0から1の範囲を取り、1に近づけば近くほど、回帰式の精度が高いと言える。
回帰式)
目的変数(y)を説明変数(x)を使って表す式を回帰式(回帰方程式・予測式)と呼ぶ。単回帰分析の場合、通常、y=a+bxの一次方程式となる。aが切片、xが説明変量、yが目的変量、bが回帰係数(傾き)と呼ぶ。また、上図の散布図の中の直線(回帰直線)は、散布図の各点からもっとも距離が短くなるように引かれた線を指す。これは、最小二乗法を使って求める。なお、3つ以上の変数を用いて目的変数(y)を説明しようとすることを重回帰分析と呼び、その時の回帰式は、y=a+bx1+cx2となります。x1,x2は説明変数を、b,cは偏回帰係数を表す。そのほかにも、非線形回帰分析では成長曲線やロジスティック曲線を使用する。
相関関係と因果関係について)
一方が増えると他方も増える場合、相関関係(別々の出来事が同じタイミングで起こった関係性)があるといえるが因果関係(結果に対する直接の原因となっている関係性)まであるといえないケースが多々あります。
上記の例)アイスクリームの売上が増えた、そして、ビールの売上が増えた…
この現象に対して、アイスクリームとビールという2つの増加には相関関係があるが、因果関係は別の要素が関係していることがあります(この例の場合は気温が原因となり、これを交絡因子と呼ぶ)。相関関係と因果関係の見極めは重要です。ただし、因果関係を掴むことは容易ではないため、まずは、相関関係なのかどうかを区別するだけでも良いと考えます。
余談ですが…
https://ddnavi.com/news/237845/a/
上記の資料によると、東大合格者という条件のもと、水泳を習っていた割合が65.8%と記載されております。これをみて、水泳やらせておけばもしかしたら東大に入っちゃうかもしれない、という幻想を抱いてしまいそうですが果たしてこの幻想は正しいでしょうか。もし、東大合格者という条件のもと水泳を習っていた割合と東大以外の合格者で水泳を習っていた割合がほぼイコールであれば、水泳と東大合格は「独立」(=無相関)しているといえます。
なお、下記の条件が成り立つ時、「独立」しているといえます。
・P(A|B) = P(A)
→ Bという条件のもとAが起こる確率と条件関係なくAが起こる確率が等しい
・P(A|B) = P(A|not B)
→ Bという条件のもとAが起こる確率とB以外の条件のもとAが起こる確率が等しい
b) 外れ値について
外れ値とは、極端に大きな値または小さい値を指します。異常値として捉える場合もあります。算術平均はこの外れ値に影響を受けやすいことは前述した通りです。ここでは外れ値の見つけ方を総括します。
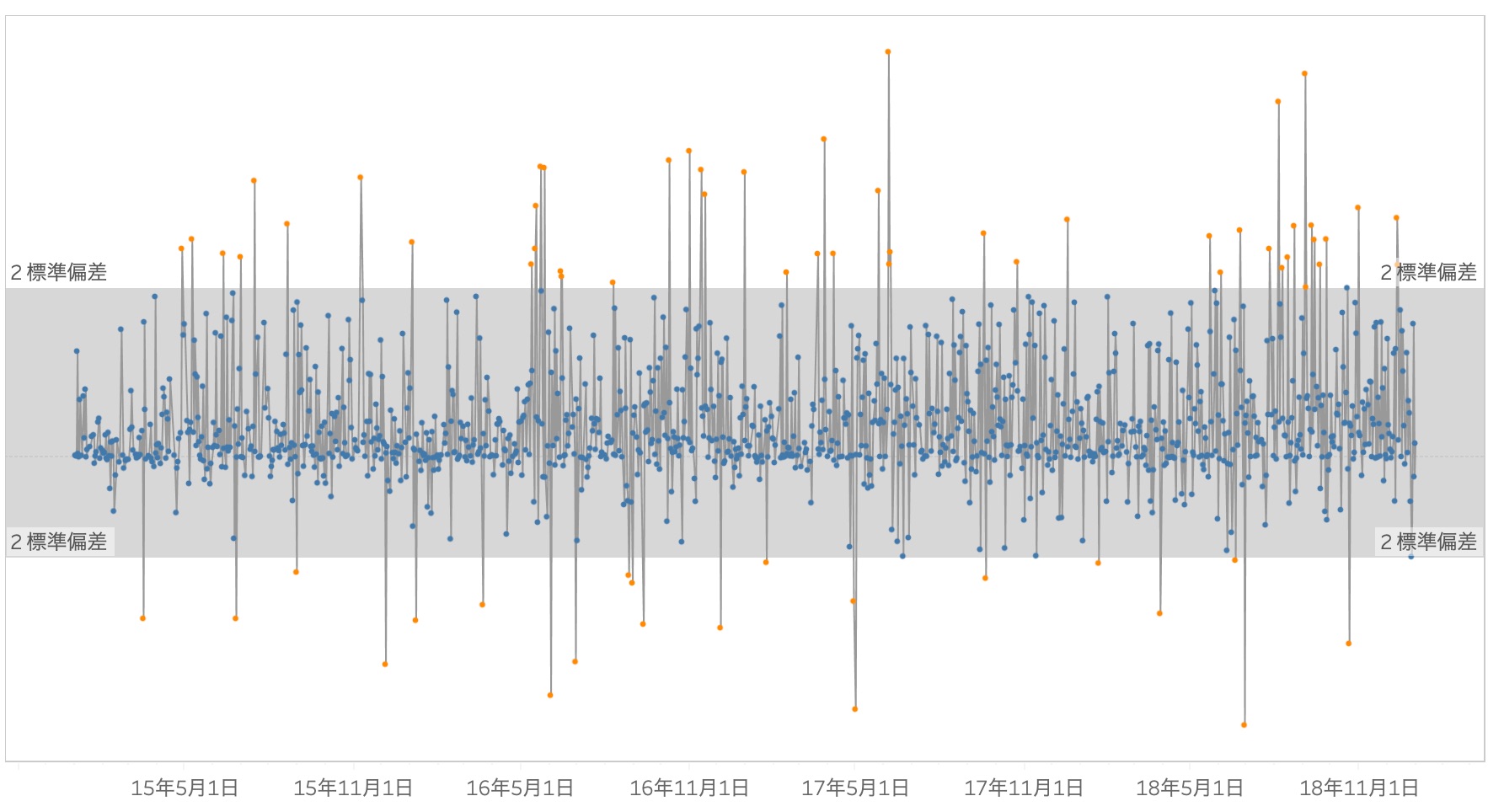
・2標準偏差を使って外れ値を探す
2標準偏差の間には約95%のデータの値が入るため、そこから外れた5%の値を外れ値としてみなします。さらに厳しい条件を設定する場合は3標準偏差を使います。3標準偏差は約99.7%のデータの値が入るため、そこから外れた0.03%のデータの値を外れ値とする方法もあります。
・IQRを使って外れ値を探す
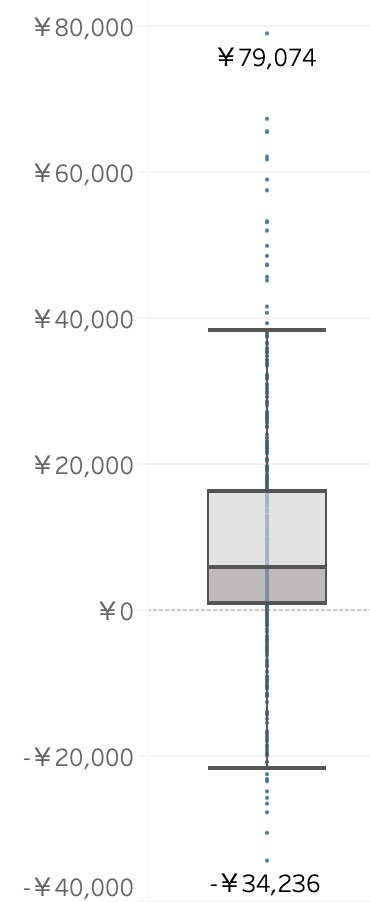
下記の箱ひげ図の上ひげと下ひげを超えるデータの値を外れ値とみなす方法です。なお、箱(Box)の上端のラインが75パーセンタイル(第三四分位数)であり、データの小さい方から数えて75%の位置に該当します。他方、箱の下端のラインが25パーセンタイル(第一四分位数)となり、データの小さい方から数えて25%の位置に該当します。そして、第三四分位 – 第一四分位 = IQRと呼びます。また、IQRの範囲はデータ全体の50%が分布していることになります。最後に、上ひげと下ひげはこのIQRを1.5倍したのち、第三四分位に足すあるいは、第一四分位から引いて算出された地点を取ります。また、この場合、上ひげと下ひげの長さは同じです。
第一四分位(1Q):箱(BOX)の下端ラインが25パーセンタイル点
第二四分位(2Q):箱(BOX)の中央ラインが50パーセンタイル点
第三四分位(3Q):箱(BOX)の上端ラインが75パーセンタイル点
IQR:3Q -1Q
1.5IQR:1.5*IQR
外れ値:第一四分位 – 1.5IQRを下回るまたは、第三四分位+1.5IQRを上回るデータ値
(7)サンプル・母集団・標本誤差・確率・正規分布・確率密度関数
a) サンプル(標本)
母集団から無作為に取り出されたデータあるいは、実験や調査で入手したデータ。
b) 抽出(サンプリング)
母集団からサンプルを取り出すことを「抽出」と呼ぶ。また、でたらめに抽出することを「無作為抽出」と呼ぶ。
c) 母集団
対象の全体あるいは、サンプルから統計的な分析を実施して推測する対象全体を母集団と呼ぶ。なお、母集団あるいはサンプル(標本)のデータ数を「サイズ」と呼びます。これを母数と呼ばない点がポイント。
例)選挙の当選速報
母集団 =有権者のうちの投票者 ※ 基本的には自分で決定する
調査手法 =標本調査(出口調査)
例)新入社員全員の意識調査
母集団 = 新入社員全員(=標本)
例)新入社員の一部の社員の意識調査
母集団 = 新入社員全員
標本 = 無作為に抽出された新入社員の一部のアンケート回答者
d) 標本誤差
無作為に抽出されたサンプル(標本)は、標本ごとに性質が異なる。これを標本誤差と呼ぶ。この標本誤差を克服するために「確率論」を用いる。標準誤差とは異なるため、注意。
※標準誤差 = サンプルデータの標準偏差 / √ n nはサンプル数
e) 確率
確率とは、おおまかに、特定事象Aが起こる要素の個数を、全事象(結果全体)の要素の個数で割った値。
確率(p) = 特定事象Aが起こる要素の個数 / 全事象の要素の個数
標本から母集団の真の性質を推定するために確率論を用いる。抽出が「でたらめ・ランダム」であることが前提。
f) 確率変数
確率変数とは、試行することで値が確定する「変数」を指す。
例)サイコロ2つの目の和の取りうる値は2〜12。この場合、この2〜12を確率変数と呼ぶ。
確率変数には、離散型確率変数と連続型確率変数の2つがある。連続型確率変数では、確率分布の特定区間の面積を計算することで確率を求める必要がある。
g) 確率分布
確率分布とは、確率変数とそれらがとる確率を表したもの。それらを表にしたものを確率分布表と呼ぶ。なお、離散型確率変数と連続型確率変数によって確率分布を分けて考える必要がある。また、連続型確率変数の分布を表現するには、確率密度関数を利用する必要がある。
離散型確率変数の確率分布)
| 分布名 | 特徴 | |
| 離散型 | 一様分布 |
すべての確率変数の生起確率がすべて同じ確率分布。形状は長方形。例としては、1個のサイコロのそれぞれの目の出る確率など。 |
| 二項分布 |
ベルヌーイ試行をN回行った時の成功回数を確率変数Xとする確率分布。ベルヌーイ試行とは、ある事象A(当該事象)とある事象A以外の事象(余事象)の和集合(全体集合)が全ての事象となる時の試行・事象・実験。例としては、コインの表と裏、サイコロの1の目とそれ以外の目や奇数と偶数など。ある事象Aの生起確率Pとすると、ある事象A以外の事象の生起確率は1-P。 確率質量関数 f(x) = nCxPx(1-P)n-x この時のパラメータは、N、P |
|
| ポアソン分布 |
滅多に起きない事象を対象とする確率分布。二項分布を近似した確率分布。試行回数nが大きいなかで、「単位時間あたりで平均λ(ラムダ)回発生する事象」がx回発生すると考えられる確率。パラメータはλ(ラムダ)。λ(ラムダ)は平均値。eはネイピア数という定数(2.71828…)。 確率質量関数 f(x) = λxe-λ / x! この時のパラメータは、λ(ラムダ) |
連続型確率変数の場合)
| 分布名 | 特徴 | |
| 連続型 |
正規分布 |
試行回数nが大きい時の二項分布の近似分布。この正規分布に従う確率変数は非常に多い。 確率密度関数 f(x=x) = 1/√2πσ e-(x-μ)2/2σ2 この時のパラメータは、μとσ e のあとは、-(x-μ)2/2σ2 噛み砕くと下記のような式になる。 σ2:母分散、μ:母平均。 |
| z分布 | 標準正規分布。標準化した統計量zの分布(平均は0、分散は1) | |
| t分布 | 不偏分散を使ったt値の分布 | |
| x2分布 | z値をデータの数だけ平方和したx2値の分布 | |
| F分布 | 2つの母集団から取ってきたx2、もしくは不偏分散の比であるF値の分布 |
各確立分布定義の引用『入門 統計学 −検定から多変量解析・実験計画法まで−』
h) 正規分布
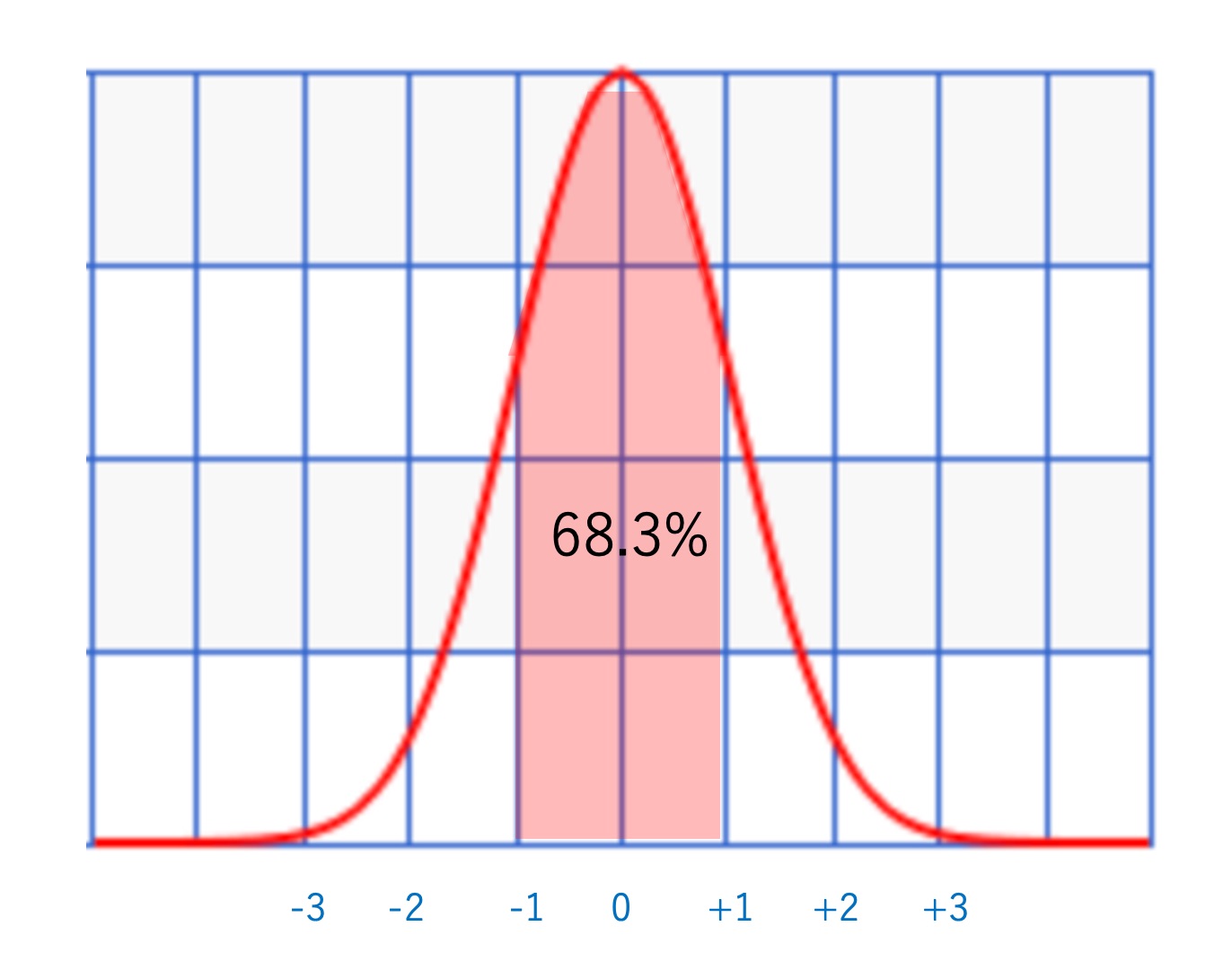
正規分布とは、平均を中心とした左右対称のつりがね型の曲線です。母集団が正規分布に従っている場合、そのサンプル(標本)も正規分布に従っているはず、と考えます。また、標準偏差が大きくなると高さが低くなり、逆に標準偏差が小さいと高さは高くなるという性質があります。
・正規分布のグラフでは、+-1標準偏差の間に、約68%(1σ範囲:0.683)のデータの値が入る。
・正規分布のグラフでは、+-2標準偏差の間に、約95%(2σ範囲:0.954)のデータの値が入る。※3σ範囲では、0.997。
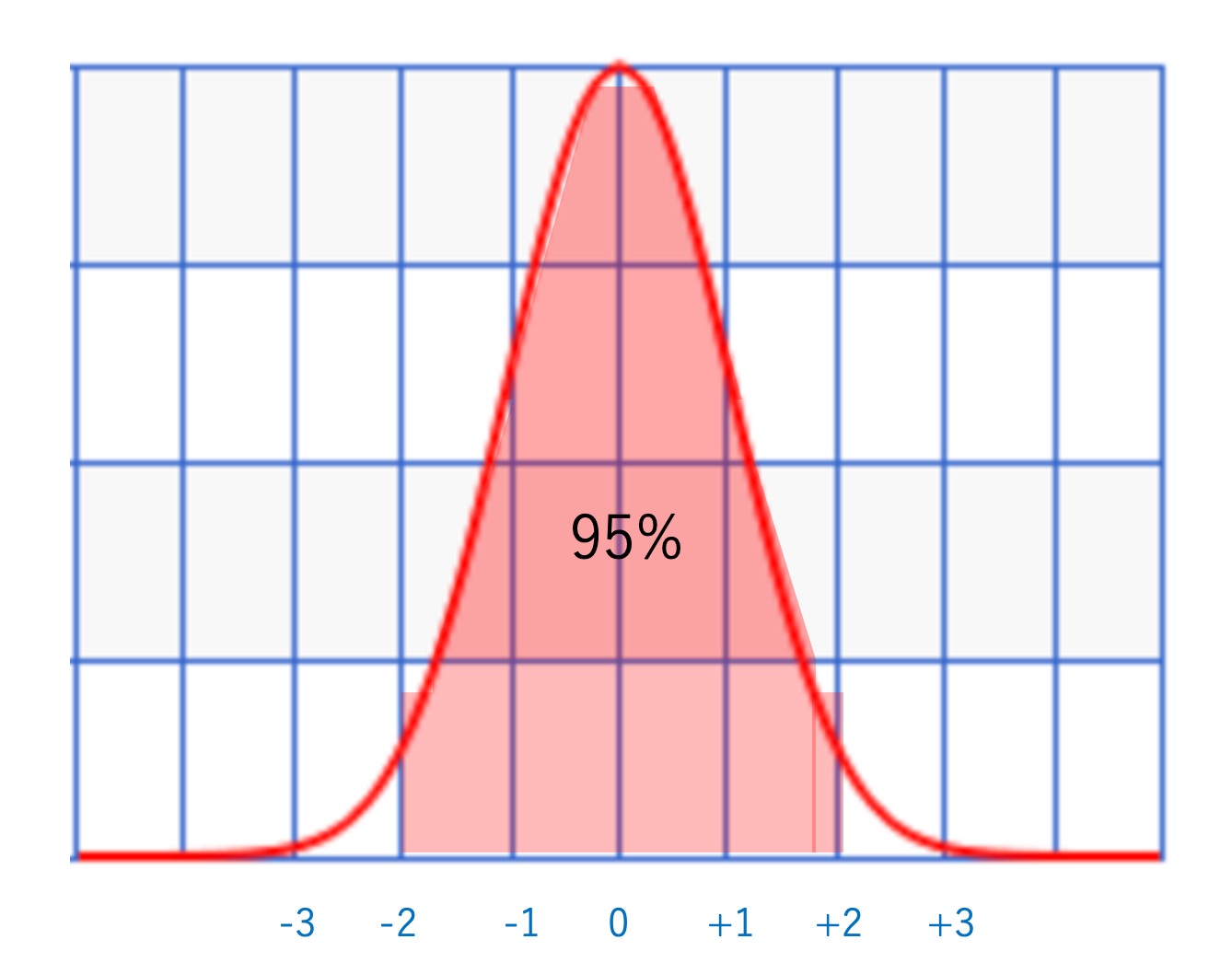
i) 確率密度関数と面積=割合=確率
確率密度関数とは、ざっくり、ヒストグラムにおける階級幅を限りなく狭めた曲線の式を指し、下記のとおりとなります。
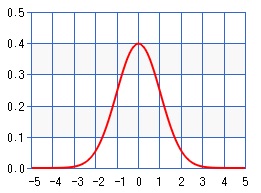
平均が0、標準偏差が1とする場合、xは、平均が0で標準偏差が1の正規分布(=標準正規分布)に従うといいます。そのときのグラフは下記図の通りです。
標準正規分布
データ正規化(基準化)したあとの結果は、上記の標準正規分布に従うといえます。そして、この場合のグラフの全体の面積は1となります。この標準正規分布では、平均からnσ離れた範囲の面積は、μやσに寄らず、一定であるという性質があります。
※ データ正規化 = 平均を0、標準偏差を1に変換すること
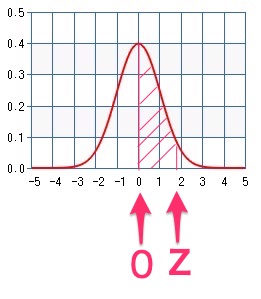
このとき、0からZの範囲の面積は、「標準正規分布表」から求まります。
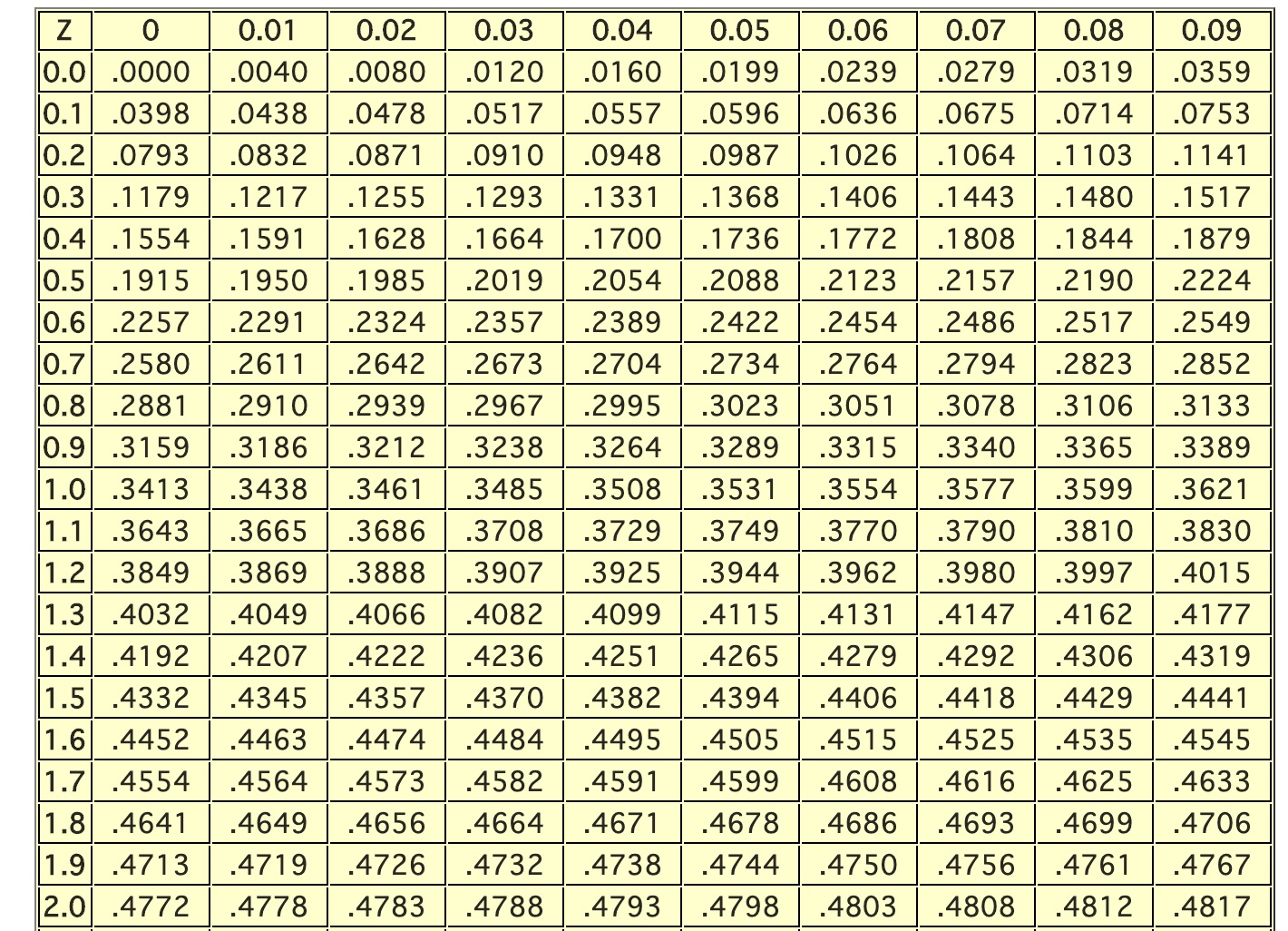
例えば、Zを仮に1.96とした場合、下記の標準正規分布表の縦軸1.9と横軸の0.06の交差地点の0.475が0-1.96の範囲の面積となります。また、0.475を2倍すると0.95となります。なお、全体面積の1から0.95を引くと0.05となります(1-0.95=0.05)。この面積の0.95は、割合(95%)・確率(95%)といいかえることができます。
上記表から、下記のσ範囲が定義できますが、信頼区間の定義と密接に関わってきます。
1.64σ範囲:0.4495 (0.90)
1.96σ範囲:0.4750 (0.95)
2.58σ範囲:0.4951 (0.99)
(8)中心極限定理
中心極限定理とは、サンプル(標本)n が増えれば増えるほど…
① 正規分布の形に近づき、
② 分布のばらつき自体も小さくなり高さが高くなる(1/√n)
③ 標本平均x–の平均は母平均μと一致
④ 標本分散は、母分散σ2をnで割った値となる(σ2/n) *標本標準偏差=σ/√n
サンプル数1と比較して…
・サンプル数 10の場合 → 1√10 → 1/3.16 → 0.31倍ばらつきが小さくなる
・サンプル数 100の場合 → 1√100 → 1/10 → 0.1倍ばらつきが小さくなる
つまり、標本平均のサンプル数(標本)が大きくなればなるほどばらつきが小さくなり(=信頼区間の幅が小さくなる)、結果、母平均に限りなく近づくということになる(大数の法則)。
(9)標準誤差・95%信頼区間
a) 標準誤差
標本から母集団の性質を推定するとき、その統計量を推定量と呼びます。標本と母集団は性質を少なからず異にするため、その推定量は少なからず誤差を含みます。その誤差を、推定量の標準偏差=標準誤差として定義します。
標準誤差 = サンプルデータの標準偏差 / √ サンプル数(平方根)
b) 95%信頼区間
95%信頼区間とは、母集団の平均(母平均μ=確定値)を跨ぐ範囲(区間)を指します。いくつかのサンプルの平均値をとった場合、母集団の平均値(母平均μ=確定値)に完全一致することはほぼないです。そこで、母集団の平均(母平均μ=確定値)はこれくらいの範囲(区間)にほぼ収まるだろう、という範囲(区間)で推定するようにします。信頼区間の推定を繰り返す過程において、95%が、母集団の平均(母平均μ=確定値)をまたぐ(含む)、と解釈できます。
・平均値を中心に考える場合(両側)
95%信頼区間 = サンプルデータの平均 – 1.96*標準誤差 ≦ 母平均 ≦ サンプルデータの平均 + 1.96*標準誤差
※ 標準誤差に2をかけるのではなく、1.96をかけるのが正しい。
・左側から右側に向けて(あるいは右側から左側に向けて)95%の範囲を考える場合(片側)
95%信頼区間 = サンプルデータの平均 + 1.64*標準誤差
95%信頼区間 = サンプルデータの平均 – 1.64*標準誤差
(10)仮説検定・P値・過誤 etc
仮説検定
仮説検定とは、母集団分布に関する仮説をサンプル(標本)から検証・推定する統計学的方法を指します。
仮説検定の基本的な流れ
仮説検定のアプローチとしては、①帰無仮説を立てる、②対立仮説を立てる、③有意水準を確認、④検定統計量の分布を確認、⑤棄却域の確認、⑥実験、⑦判定(滅多に起きないことが起きた…) となります。そして、帰無仮説が矛盾していることを証明して帰無仮説を棄却する流れで展開します。
a) 帰無仮説
証明したい仮説と相反する仮説(=本当は棄却したい仮説)を帰無仮説と呼びますが、最初にこの帰無仮説を立てます。一般的には、AとBで差はなかった、という形式になります。この帰無仮説を立てることが仮説検定のスタートになります。
例)証明したい仮説 Aは、Bよりも効果が高かった
帰無仮説 AとBでは効果に差はなかった
もし、帰無仮説が成り立つ場合、Aの平均の分布は、Bの平均の分布と同じになるはず、と考えます。
b) 対立仮説
帰無仮説が棄却された場合、代わりに「採択」される仮説を対立仮説と呼びます。一般的には、AとBでは差はないとはいえない(二重否定)の形式になります。
※ 後述する過誤との関係で回りくどい言い方をしておりますが、誤解を恐れずにいえば、差があったというニュアンスであるとざっくり捉えてよいでしょう。
c) P値と有意水準
P値とは、帰無仮説が成立しているという前提のもとで、今回得られたデータの値と同等かそれ以上に極端な値が出る確率をP値と呼びます。このP値が有意水準(5%ないしは1%)よりも小さい場合、滅多に起きないことが今回起きてしまったとして、帰無仮説は成り立たない(=そもそも前提がおかしい…)と考え棄却されます。結果、対立仮説が採択されます。
※P値 = 「差がない」という帰無仮説が正しい確率(正しい解釈ではないものの、こちらの方がイメージしやすい…)
※P値は有意差まではわかるが程度(=実際にどれくらいの差があるか)まではわからない
※差の程度は、95%信頼区間で把握する
有意水準とは、極めて稀に起こると判断できる基準を確率として設定した値を指します。通常、5%や1%が設定されることが多いです。極めて稀に起こるようなことが今回起きた場合、偶然に起こったのではなく、必然的に起こったとして有意であると考えます。帰無仮説が成立しているかどうかを判断する基準になります。
d) 両側検定、片側検定
正規分布で有意水準を5%とする場合…
帰無仮説:平均身長は150cmである…
対立仮説1:平均身長150cmと異なる →両側検定&両側合わせて5%が棄却域
対立仮説2:平均身長150cmより大きい →片側検定&右側5%が棄却域
対立仮説3:平均身長150cmより小さい →片側検定&左側5%が棄却域
e) 仮説検定の種類
・z検定:
正規分布のもと、標本の平均と(既知である)母集団の平均が有意であるかどうかを調べる
・t検定:
(ざっくり)2つのグループの平均の差に有意差があるかどうかを調べる時に使う
・F検定:
(ざっくり)3つ以上のグループの平均の差に有意差があるかどうかを調べる
・カイ二乗検定:
(ざっくり)2つのグループの割合の差(=期待値と実際の値のズレ)に有意差があるかどうかを調べる時に使う
e) 過誤
第一種過誤(タイプ1エラー):本当は差がないのに、検定の結果、差があると誤判定(帰無仮説を棄却できないのに棄却してしまった)
第二種過誤(タイプ2エラー):本当は差があるのに、検定の結果、差がないと誤判定(帰無仮説を棄却すべきなのに棄却しなかった)
f) 効果量
平均の差を標準偏差で割って標準化した値で、「差」の大きさを表す指標。2つの標本間の平均値の差を標準偏差で割って標準化したもの。
(11)統計でよく出てくる計算
① log2N 2を何乗するとNになるか?
例)log216 2を何乗すると16になるか?(A.4)
log : 対数(指数を表現したようなもの)24 = 16
2 : 底
N : 真数
4 : 指数
② Σ(シグマ) 総和
i : 始まりの定義と後式の変数を定義している
n : nは終わりを定義
Σ : 総和を意味する
上記は、1/5(X1+X2+X3+X4+X5) となる。
(12)統計でよく出てくる記号
- μ 母平均
- σ2 母分散
- σ 母標準偏差
- x- 標本平均 ※注意 エックスバー(xの上に-)
- s2 標本分散
- s 標本標準偏差
- R2 決定係数
- r 相関係数
母集団に関するもの:ギリシャ文字
標本に関するもの :アルファベット
まとめ
今回は、統計をはじめるにあたってのその最初の一歩となりそうなトピックを洗い出してみました。正確さを重視する統計学にあって、誤解を恐れずに言及した部分も数多くあります。しかし、正確さを追求するあまり、結果的によくわからなくなるというジレンマを克服したいという考えのもとですので、その旨、多少ご理解いただきたく、一歩めの手がかりとして参考にしていただけますと幸いです。